Wie verschieden gezählt wird!
Einige
Zahlensysteme
Für die Darstellung von Zahlenmengen werden generell Zahlensysteme verwendet. Die Zahlen sind nach festgelegten Regeln als Folge von Ziffern bzw. Zeichen geschrieben. Das uns bekannteste Zahlensystem ist das Dezimalsystem (Zehnersystem). Computer arbeiten im Dualsystem (Zweiersystem) und weil diese Zahlen sehr lang werden können, verkürzt das Hexadezimalsystem (Sechzehnersystem) auf einfache Weise die Dualzahlen deutlich.
⇓ Menü
Es gibt eine ganze Reihe verschiedener Zahlensysteme:
Unser gebräuchlichstes Zahlensystem. Es besitzt die Ziffern von 0,1,2,3,…9. Das liegt wohl daran, dass wir zehn Finger besitzen (Die meisten von uns jedenfalls!).
Computer arbeiten nur mit zwei Ziffern (Zuständen): 0 und 1.
Alles, was lebt (Mikroben, Pflanzen, Pilze, Tiere, Menschen) besitzen einen Gen-Code (DNA), der aus 4 „Buchstaben“ besteht: den organischen Basen (Adenin, Thymin, Guanin und Cytosin, oft abgekürzt mit A, T, G und C).
Das Zwölfer-System wird in der Geometrie und Navigation angewendet. Sein Vorteil liegt darin, dass es viele Teiler besitzt: 1,2,3,4,6,12 (siehe Torte beim Bäcker)
Trotz unseres Dezimalsystems, verwenden es alle:
- Winkelmaße: 0° – 360° (siehe auch globale Koordinaten)
- Zeit: 2 x 12 Stunden (für Nacht & Tag)
Es gibt aber keine Zeichen für die Ziffern 10, 11 und 12 – daher müssen wir umrechnen.
Inhalt
Aufbau eines Zahlensystems
Dezimalsystem
Quelle: wirtconomy | Youtube [Länge: 5:06 min.]
Eine Zahl setzt sich aus Ziffern zusammen. Die Stelle, wo sie steht ihre Wertigkeit. Dabei wird die Ziffer an der Stelle, wo sie steht mit ihrer Wertigkeit multipliziert. Das gilt für alle Zahlensysteme. Im Dezimalsystem gibt es zehn Ziffern, daher ist die Basis 10. Ihre Wertigkeit ergibt sich im von Null startenden Exponenten, der sich um jede höhere Stelle um eins erhöht.
[Klicken, um zu vergrößern]
Dualsystem
[Klicken, um zu vergrößern]
Genauso ist es bei dem Dualsystem – mit dem Unterschied, dass es nur zwei Ziffern gibt: 0 und 1. Daher ist die Basis jetzt 2 (und nicht 10). Daraus ergeben sich andere Stellenwertigkeiten. Sie springen im 2-er Rhytmus.
- Dualzahlen sind länger, als Dezimalzahlen, und Menschen können sie leicht verwechseln.
Leider gibt es für die Umrechnung von dualem und dezimalen Zahlensystem eine „inkampatibiltät“: Um alle dezimalen Ziffern zu kodieren, sind 3 Bit zu wenig – 4 Bit wiederum zu viel. Es bleiben die „Ziffern“ von 10 bis 15 übrig. Dafür verwendet das Dezimalsystem bereits zwei Ziffern!
Hexadezimalsystem
[Klicken, um zu vergrößern]
Warum Hexadezimal?
Man fasst damit auf einfache Art endlos lange Binärzahlen zusammen und verkürzt sie: z.B.
1001 1101 0010 0000 1101 1111 1001 0111 0001 0101 0010 1010 0010 0000
— > ergibt:
9 | D | 2 | 0 | D | F | 9 | 7 | 1 | 5 | 2 | A | 2 | 0
Im Hexadezimalsystem gibt es die Ziffern: 0, bis 16. Daher ist die Basis jetzt 16 (und nicht 10 oder 2). Daraus ergeben sich andere Stellenwertigkeiten. Sie springen im 16-er Rhytmus. Für die Ziffern 10-15 gibt es keine eigenen Zeichen. Daher werden Buchstaben verwendet: (A, B, C, D, E,F).
- Hexadezimalzahlen verkürzen die Schreibweise von Dualzahlen auf ein Viertel. Sie sind untereinander leicht umzurchnen und einfacher zu lesen.
Hex-Zahlen finden z.B. Anwendung:
- Farbcodes (RGB)
- IP-Adressen Version 6
- MAC-Hardwareadressen von Netzwerkkarten
Umrechnung der Zahlensysteme
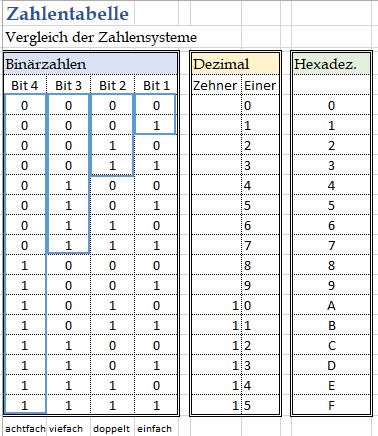
Stellt man die drei Zahlensysteme mit ihren Ziffern nebeneinander, so ergibt sich ein unterschiedlicher Bedarf an Ziffern.
[Klicken, um zu vergrößern]
- Solange die Ziffern in allen Zahlensystemen vorhanden sind, werden sie auch so verwendet.
- Da es keine Ziffern für die 10, 11, 12, 13, 14, 15 gibt, werden statt dessen im Hexadezimalsystem Buchstaben von A…F verwendet.
- Hier sieht man deutlich, dass mit 3 Bit nur die Ziffern bis 7(dez) codieren, mit 4 Bit aber einige Ziffern unbesetzt bleiben.
- Die beiden Systeme Dual und Hex passen zueinander. Die Umrechnung ist denkbar einfach (siehe unten).
Welchen Rhytmus (oder kleine Regel) kann man sich merken, damit man eine vollständige Tabelle – ohne viel nachdenken – leicht selber erstellt?
Binär - Dezimal
[Klicken, um zu vergrößern]
- Binäre Zahl hinschreiben,
- Darunter von links je Stelle aufsteigend 1,2,4,8,16,32,64, … darunter schreiben.
- Alle Zahlen addieren in der die Ziffern der binären Zahlen „1“ sind.
- fertig.
Dezimal - Binär
[Klicken, um zu vergrößern]
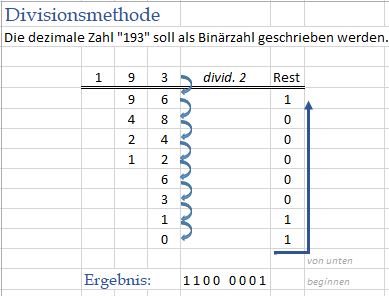
- Dezimale Zahl hinschreiben,
- solange immer wieder durch 2 teilen, bis man bei Null anlangt.
- Ist die Zahl gerade, ergibt sich ein Rest Null.
- Ist die Zahl ungerade, Rest Eins notieren und nächst kleinere Zahl weiter teilen.
- Wenn fertig, die REST-Zahlen von unten nach oben aufschreiben
- fertig.
HINWEIS: Es gibt noch eine andere Methode, die für kürzere Binärzahlen sogar etwas einfacher ist. Sie heißt „Differenzmethode“.
Hexadezimal - Binär - Hexadezimal
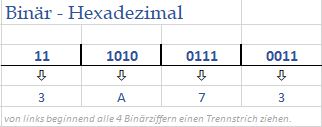
Erklärt sich von selbst?!
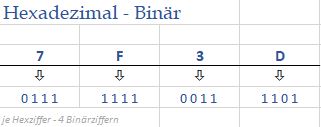
Hexadezimal - Dezimal
Es gibt zwei Möglichkeiten:
- Umrechnung mit Basis 16 (wie im Bild links)
- Umrechnung ins Dualsystem, dann von Dual ins Dezimalsystem.
Binäres Rechnen - Bsp. Addition
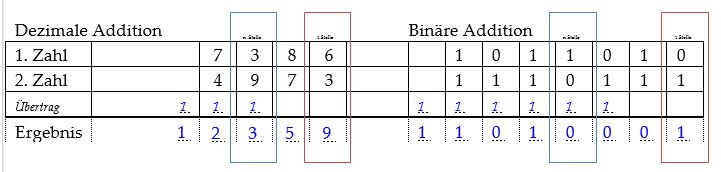
Die Vorgehensweise ist eingentlich identisch, nur im Binärststem ist nach „1“ schon schluss, und man beginnt wieder mit „0“. Damit kommt ein Übertrag viel schneller vor.
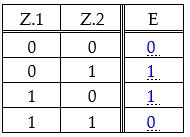
Die Wertetabelle zeigt alle Zustände, die in einer Spalte vorkommen. Ein Übertrag wird nicht berücksichtigt. Das nennt man:
Halbaddierer
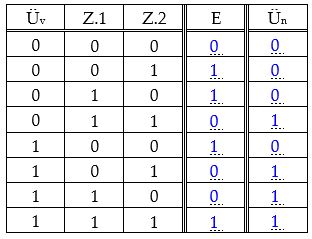
Eine Wertetabelle, die den Übertrag sowohl von der vorherigen als auch in die nächste Stelle berücksichtigt, nennt man:
Volladdierer
10 Wiederholungsfragen
Dualsystem: Computer; Vierersystem: Biologie/Natur; Zwölfersystem: Geometrie/Navigation; Hexadezimalsystem: Kurzschreibweise Dualsystem.
mindestens 4 Binärstellen.
Das Hexadezimalsystem hat 16 Ziffern: 0,1,2, …,9, A,B,C,D,E,F
1110 – binär, oder 14 dezimal.
von rechts anfangen, nach links gehend (gegen Leserichtung) 4er Gruppen bilden.
Mit der Null, danach die Eins. Jede Spalte das Doppelte der vorgehenden Spalte.
1111 1110 = 8 Bit/1Byte
Ergebnis 1, Übertrag 1
Halbaddierer berücksichtigen keinen Übertrag.